用神经网络压缩图像
简介
图像压缩，尤其是视频压缩，是一个具有明显现实意义的问题，视频流量占所有互联网流量的 60% 以上。多年来，人们开发了越来越多的无损和有损编解码器来解决这一问题。最近，出现了使用自动编码器式神经网络进行压缩的新兴研究领域。本篇文章将介绍这一领域的演变过程，并重点介绍该领域的发展方向。
JPEG
要了解神经压缩，我们首先需要了解自 1992 年以来无处不在的 JPEG 标准。无损编解码器利用了数据中的统计冗余：如果你能根据前一个字节的情况预测下一个字节，那么在编码器和解码器中使用相同的统计模型，就能为更可能出现的字节分配更小的编码，从而提高压缩率。有损编解码器则更进一步，完全忽略一些 “不太重要 “的数据。
网上有很多关于 JPEG 的精彩教程，比如这个，但最重要的启示是，人眼对边缘等低频变化的接受能力要比对精致纹理等高频变化的接受能力强得多。艺术家们利用这一点，创造出一种 “细节的错觉”，而不是真正绘制每一片草叶。
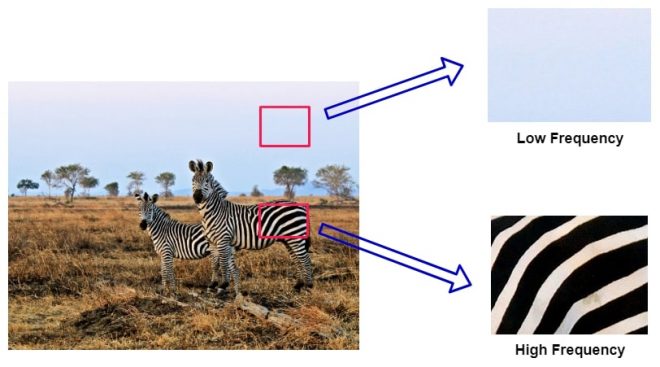
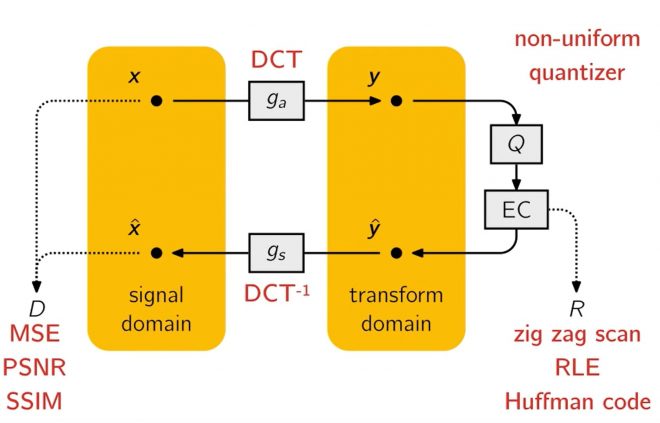
JPEG 利用了这一点，使用离散余弦变换将图像数据转换到频域，将图像的每个 8×8 像素块表示为具有不同频率和振幅的余弦函数之和。而不是 H×W 空间像素，我们剩下的是 H×W DCT 系数，其中每个 8×8 的系数块对应图像的一个块。
接下来，8×8 的数值块被一个 8×8 的量化表逐个元素分割，然后对结果进行四舍五入（这就是 JPEG 有损压缩的原理）。直观地说，在保存 JPEG 文件时，只要降低质量设置，就会增加量化表的值，从而在图像的最终表示中出现更多的零，使其更容易压缩。值得注意的是，量化表中的值并不是统一的，也不是随机的，它们都是经过精心挑选的，以提供令人愉悦的视觉效果。事实上，这些表格并没有什么特别之处，任何软件或用户都可以根据需要更改其数值。
由此产生的量化频率值就是图像的压缩表示。在实际应用中，这将通过无损编码进一步压缩（所有舍入的零都是多余的），我们这次将跳过这一点。但值得注意的是，DCT 和量化是可逆操作，因此我们可以在解码器阶段对它们进行逆操作，从而对原始图像进行有损重建。
JPEG 内部结构高级示意图
上面这张幻灯片来自约翰内斯-巴莱（Johannes Ballé）在 2018 年的演讲，从高层次总结了 JPEG。令人震惊的是，这与神经网络图何其相似–我们有一个自然损失函数和两个（线性）变换及其逆变换。一个自然而然的问题是，这样的系统是否可以通过这样的变换参数化进行端到端训练：
图像编解码器内部结构示意图
自动编码器层出不穷
那么，为什么我们不能训练任何自动编码器，使其MSE最小化，然后一劳永逸呢？通过将图像数据投射到某个低维瓶颈处，我们可以直接将其用作编码表示，对吗？
比特嵌入
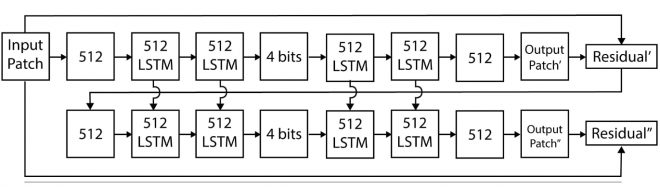
这几乎就是最初的迭代尝试。例如，在文献[7]中，作者将瓶颈限制为二进制表示。这样做的另一个好处是，矢量可以直接序列化，比特率可以直接从瓶颈大小中估算出来。
利用 LSTM 进行渐进式比特编码，[7]
在这里，自动编码器递归生成图像的 4 位（请记住，作者压缩的是 32×32 的微小图像！）表示，并将重构后的残差输入下一层等。这样重复 16 次，我们就能生成一个 64 位的矢量传输给接收器。这意味着该方法也是首批具有自适应速率控制的方法之一，而这正是编解码器所需要的特性。
遗憾的是，这种方法在实际应用中并不能达到最佳压缩率。这是因为实际压缩率主要取决于源文件的香农熵。由于这种自动编码器没有降低潜在矢量熵的动力，因此从比特率-失真权衡的角度来看，我们的压缩效果可能并不理想。
端到端训练
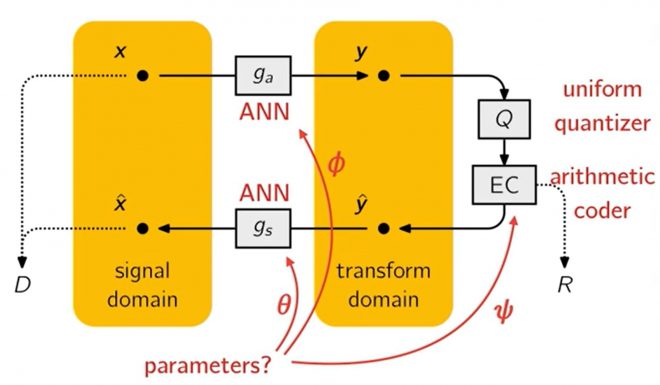
2017 年，[1] 设计出首个端到端训练模型，直接优化了速率-失真权衡，取得了开创性突破。他们的主要见解如下：
- 使用形式为 L=R+λD 其中 R 代表比特率，D 代表失真（如 MSE），从而实现两者之间的最佳权衡（对于给定的λ调节权重）。
- 要估算 R我们可以利用实际压缩率与实际熵值非常接近这一事实，因此我们只需训练一个量化潜变量的概率模型即可。
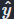=round(y)的熵直接给出比特率：
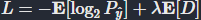其中
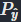是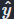. 请注意，损失中的两个项都取决于概率模型，因为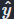也用于解码图像。 - 一种特殊的无损编码–自适应算术编码–用于实际压缩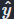压缩成比特流。无需赘述，关键在于算术编码器和解码器都取决于符号的概率分布（这里的符号是指)
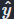这种新模型的压缩率比 JPEG 甚至 JPEG2000 都要高。
Hyperprior
一旦 R+λD 损失变得普遍后，提高压缩率的最佳方法显然是改进熵（概率）估计。另一种方法是通过算术编码器来看待这个问题：假设我们正在对英文文本进行编码。对于 “a quick brown fox jumps o “这个老掉牙的输入示例，如果我们使用静态概率模型，那么最有可能的下一个字符总是空格。但是，如果我们能使用一些 GPT 类型的上下文感知下一个字符预测器，它就能利用已有的信息，实现更好的压缩率。请注意，编码器和解码器需要使用相同的模型。
[2] 也做了类似的工作。当之前的概率模型是固定的（基本上反映了所有训练集图像中潜在字符的预期分布），现在我们发射一个额外的量化通道
也作为比特流发送。然后，接收端首先解码的分布参数。y 的分布参数（实际上，每个元素 yi 建模为高斯分布），然后解码的条件，这意味着概率模型变得与图像相关。
开创性的超前沿网络，[2]。在上文中，GDN 只是另一种非线性，可以用 ReLU 代替
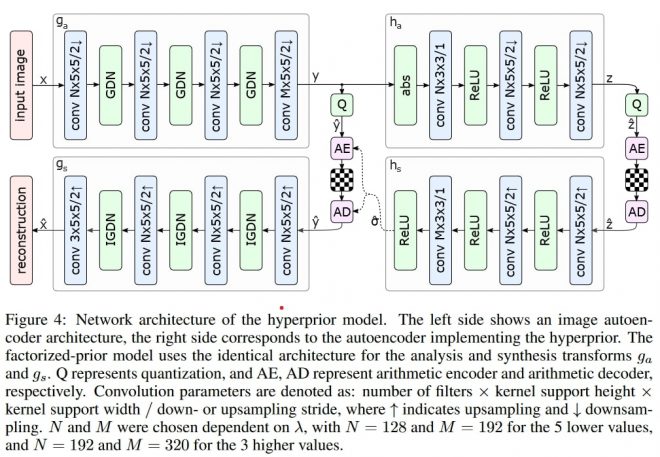
我使用流行的 CompressAI 库（您可以在这里找到一个笔记本）对 hyperprior 模型进行了一些尝试。我使用一个包含 100k 幅 96×96 图像（STL-10）的玩具数据集，在不同的 λ 值训练一个微小的玩具模型，并记录平均熵和 MSE 损失。虽然这还不足以打败 JPEG，但它展示了在实践中如何进行速率失真训练。
下面是一些有趣的图片，展示了公羊在训练过程中逐步改进的过程：
不出所料，λ 值越低 ，模型就越倾向于压缩，而值越高，我们就越能真实地重建原始图像（上图）。
自回归先验
超先验分析表明，向算术编码器的概率模型输入额外信息可以提高压缩率，即发送图像特定的 但还有其他信息我们没有使用。例如，假设我们正在解码 逐个像素解码。在前半部分之后，我们可以清楚地看到一只狗的一半。那么剩下的一半就很有可能是狗的后半部分。我们可以利用这一信息更新概率模型–只要编码器和解码器都进行这种同步顺序处理，我们就能获得较低的压缩比。
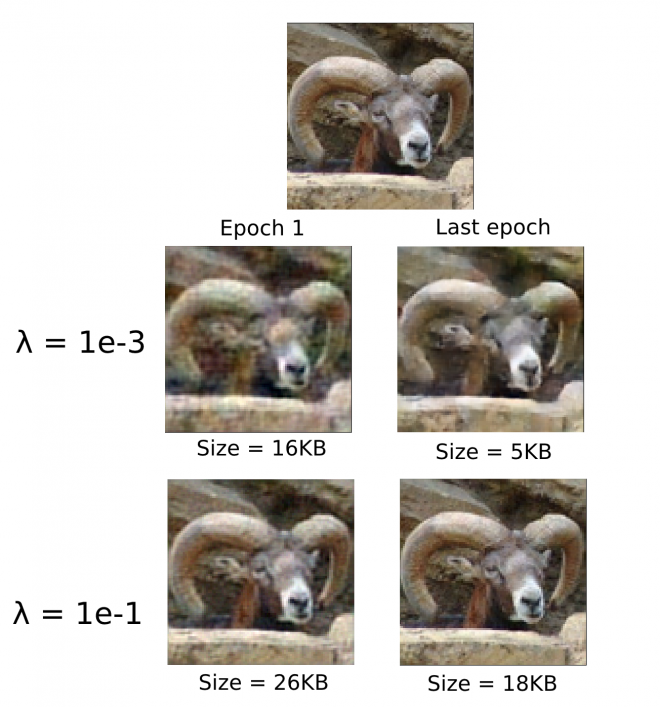
这几乎就是自回归先验背后的理念：我们不是一次或两次解码所有潜变量（如超先验），而是递归地预测下一个潜变量在前一个潜变量条件下的概率分布。算术解码器可以在每次迭代中进行调整，以优化单个潜点的打包/解包。在实践中，我们不使用之前的所有潜点，而只使用像素的局部邻域（如 5×5），这样在连续处理时就能得到 12 个像素：
图像解码 [8]
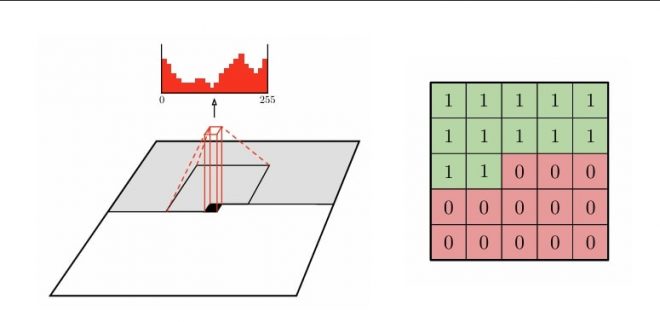
这种方法为学习型图像压缩又增加了一步改进。不幸的是，正如你可能已经知道的那样，逐个像素迭代整个图像在计算上是非常无效的。我记得在一些论文中，有人声称 95% 以上的解码时间都花在了自回归模型上！这使得该方法主要用于学术研究，在比赛中仅测量速率失真性能，没有计算限制。进一步的研究试图优化这一明显的瓶颈。例如，使用类似棋盘式上下文模型的方法可以将解码速度提高 40 多倍，而性能却不会有太大的下降：
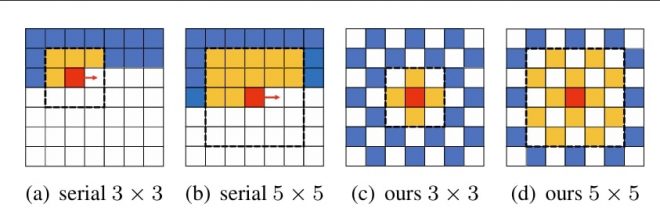
用于算术解码的棋盘语境 [4]
可变速率控制
针对 R+λD 损耗训练的模型的一个明显弱点是，我们需要为速率-失真曲线上的每个点训练一个单独的模型。这就意味着，如果您在流式传输视频，服务需要根据您的带宽（动态）存储 N 个不同的模型–这太荒谬了。传统的编解码器可以像 JPEG 中的质量设置一样，随时调整速率。
幸运的是，有一个小技巧可以在一个模型中支持可变速率。很明显，要支持这一点，我们应该使用可变值的 λ 但这些值应该与一些输入特征相结合，告诉模型我们处于哪种速率-失真机制。在 [3] 中，通过引入一个 “增益 “单元及其倒数，我们很好地做到了这一点。这是一个可学习的类似嵌入的向量，它与编码的潜在 y 的乘数，而解码则相反。
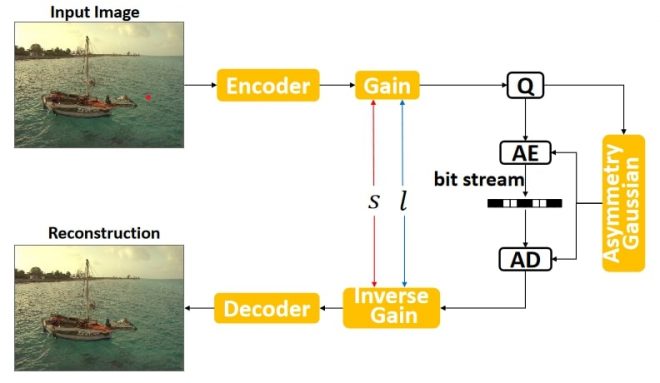
如果我们回想一下 JPEG，这与针对不同的期望质量值使用不同的量化表非常相似，但它有一个额外的好处，即增益系数和反增益系数是端对端训练的。在训练过程中，我们可以将 λ 和增益向量的范围，比如 100 个值。每个样本在 100 个样本中被分配一个统一随机的索引，并使用相应的增益向量和 λ 系数。在推理过程中，我们可以改变希望使用的 100 个增益向量中的哪一个，由于这些增益向量是经过训练的，因此我们可以有效地获得像 JPEG 一样的 1-100 质量指标！
感知损失
在图像重建中，像素方向的 MSE 通常被用作第一个简单的损失函数。然而，这在低比特率条件下会造成不必要的伪影：比方说，你有一个完美的图像重建，但它向右偏移了 5 个像素。MSE 会促使模型倾向于混合虚无，而不是这种略微错位的重建。这将导致模型在低比特率下混合出精细纹理。基于 MSE 的 PSNR 损失度量与其他更先进的度量（如 VMAF）不同，它与实际的黄金真相主观测试分数的相关性不高。一个有趣的事实是，VMAF 曾获得艾美奖的技术和工程奖：)
有哪些更具感知性的损失函数已被采用？一种相当简单的改进方法是通过输入的显著性图谱对 MSE 进行加权：可以合理地假设，与微小的背景细节相比，观众更关心人脸的重建质量。此外，我们还尝试使用像素级 L1 损失和 Charbonnier 损失来减少 MSE 造成的模糊伪影。
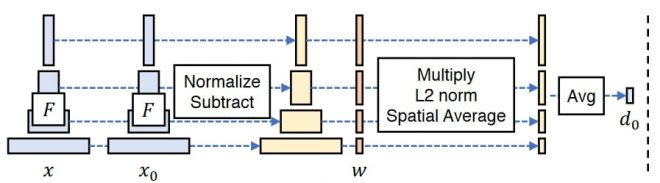
由于深度神经网络在训练过程中会从图像中提取语义信息，因此可以通过预训练网络传递图像，提取深度特征激活，并比较它们之间的距离，从而获得语义相似性度量。这就是 PIPS loss 的作用，它最初使用 VGG 网络来提取深度特征。
与 PIPS 损失类似的另一种方法是从风格转移文献中借用的风格损失。它同样从 VGG 等预训练网络中提取中间层激活，但计算公式略有不同，侧重于特征图的全局统计，旨在衡量风格差异。
在 [2] 中，作者指出可以将图像压缩方法视为生成变异自动编码器，即 λ→∞. 因此，许多在该领域有用的方法也被用于图像压缩也就不足为奇了。NeurIPS 的另一篇论文[5]表明，使用经典的图像生成方法，即 GAN 识别器，对训练图像压缩模型非常有用。事实上，根据人工评估，在比特率只有一半的情况下，根据 MSE、LPIPS 和 GAN 损失联合训练的模型被认为优于 BPG（当时最先进的基于 HEVC 视频编解码器的图像压缩器）。
挑战
图像编解码器比较，CompressAI
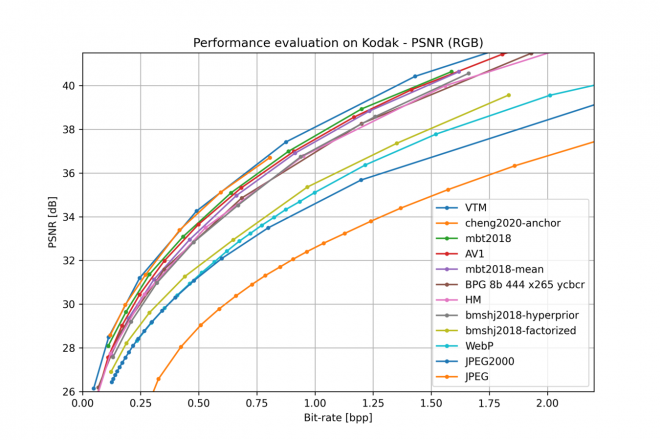
上图来自 CompressAI，显示了各种学习型图像编解码器与传统编解码器（如 VTM、AV1 和 BPG）的对比情况。虽然这些编解码器已经有些过时，但可以看出，最优秀的学习型编解码器与传统编解码器的进度不相上下。
这一点在 CLIC 压缩挑战赛中得到了证实，尤其是在视频赛道中，获胜的作品往往是混合方法，即传统编解码器与神经后处理层（内循环滤波器）相结合。这种组合方法的功效表明，神经方法的优势不足以使传统编解码器过时。事实上，在最近的 CLIC2024 比赛中，图像和视频赛道的优胜者似乎都使用了最先进的 ECM 编解码器。
不过，与准确性相比，ML 编解码器的主要问题是其计算成本，CLIC2022 挑战赛的最后一张幻灯片最能说明这一点：
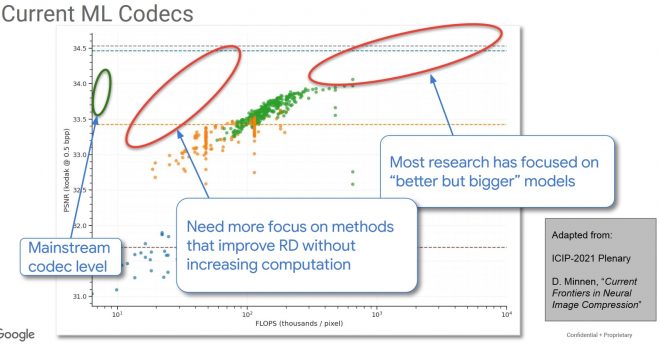Challenges in incorporating ML in a mainstream nextgen video codec
我们看到，主流编解码器与学习型编解码器在计算数量上的差距可达两个数量级。在 CLIC 挑战赛中，我们经常看到神经编解码器的解码时间比主流编解码器长 10 倍，即使它们的推理可以在 GPU 上运行。
因此，这可能意味着至少在目前，更轻量级的混合神经方法是增强图像和视频压缩的最佳途径。尽管如此，从长远来看，由于惨痛教训的影响，概念上简单得多的神经编解码器（JVET 编解码器文档动辄数百页：），以及能在通用神经硬件上运行的神经编解码器（这种硬件正变得越来越常见）很可能会占上风。至少可以肯定的是，未来好的压缩系统至少会包含一些学习组件。
参考文献
[1] Ballé, Johannes, et al. “Variational image compression with a scale hyperprior.” arXiv preprint arXiv:1802.01436 (2018).
[2] Ballé, Johannes, Valero Laparra, and Eero P. Simoncelli. “End-to-end optimized image compression.” arXiv preprint arXiv:1611.01704 (2016).
[3] Cui, Ze, et al. “Asymmetric gained deep image compression with continuous rate adaptation.” Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. 2021.
[4] He, Dailan, et al. “Checkerboard context model for efficient learned image compression.” Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. 2021.
[5] Mentzer, Fabian, et al. “High-fidelity generative image compression.” Advances in Neural Information Processing Systems 33 (2020): 11913-11924.
[6] Minnen, David, Johannes Ballé, and George D. Toderici. “Joint autoregressive and hierarchical priors for learned image compression.” Advances in neural information processing systems 31 (2018).
[7] Toderici, George, et al. “Variable rate image compression with recurrent neural networks.” arXiv preprint arXiv:1511.06085 (2015).
[8] Van den Oord, Aaron, et al. “Conditional image generation with pixelcnn decoders.” Advances in neural information processing systems 29 (2016).
[9] Zhang, Richard, et al. “The unreasonable effectiveness of deep features as a perceptual metric.” Proceedings of the IEEE conference on computer vision and pattern recognition. 2018.
本文文字及图片出自 Compressing images with neural networks
