解码为什么 JS 中的 0.6 + 0.3 = 0.89999999999999 以及如何解决?
在 Hacktoberfest 期间,我在一个开源计算器软件仓库工作时,发现某些小数计算没有产生预期的结果,比如 0.6+0.3 的结果不会是 0.9,于是我在想是不是代码出了问题。但进一步分析后发现,这是 JavaScript 的实际行为。于是深入研究,了解其内部工作原理。
在这篇博文中,我将与大家分享我的见解,并讨论几种解决方法。
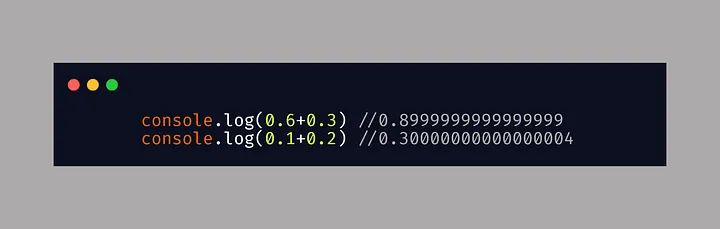
在日常数学中,我们知道 0.6 + 0.3 相加等于 0.9,对吗?但当我们使用计算机时,结果却是 0.89999999999999。令人惊讶的是,这种情况不仅发生在 JavaScript 中,在 Python、Java 和 C 等许多编程语言中也同样存在。此外,这不仅仅是这个特定的计算。还有很多十进制计算也会出现类似的错误答案。
为什么会出现这种情况?
这与计算机如何处理浮点数有关。十进制数使用一种名为 IEEE 754 标准的格式存储在计算机内存中。IEEE 754 浮点标准是当今计算机中最常用的实数表示法。该标准包括不同的表示类型,主要是单精度(32 位)和双精度(64 位)。JavaScript 遵循 IEEE 754 双精度浮点标准。

双精度由 64 位组成,包括 1 个符号位、11 个指数位和 52 个尾数(小数部分)位。
任何十进制数都只能以这种双精度 IEEE 754 二进制浮点格式存储。计算机系统中的有限 64 位表示法无法准确表达所有十进制数值,尤其是那些具有无限十进制扩展的数值,这导致在处理某些二进制数时,结果会出现细微差异。
让我们通过一个例子来了解十进制数的存储方式,并揭示为什么 0.6+0.3 等于 0.89999999999999
用 IEEE 754 双精度浮点格式表示 0.6。
# 第 1 步:将十进制 (0.6)₁₀ 转换为二进制表示base 2
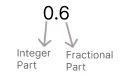
整数部分: 0/2 = 0
小数部分:
重复乘以 2,注意结果的每个整数部分,直到小数部分为零。

0.1 不能精确地表示为二进制分数。高亮部分无休止地重复出现,形成一个无穷序列。此外,我们也没有得到任何零分数部分。
![]()
# 第 2 步:归一化
如果小数点左边有一个非零的数字,那么用科学计数法写出的数字 x 就被归一化了,也就是说,强制其尾数的整数部分正好为 1。
我们根据 IEEE 标准的要求调整我们的序列,包括 52 位尾数和四舍五入的有限数量。这就是出现舍入错误的原因。
![]()
#步骤 3:调整指数:
对于双精度,-1022 至 +1023 范围内的指数偏差通过添加 1023 来获得。
exponent => -1 + 1023 => 1022 用 11 位二进制表示数值。
(1022)₁₀ => (010111111110)₂
符号位为 0,因为 0.6 是正数。(-1)⁰=> 1
现在,我们可以用 IEEE 754 浮点格式表示所有数值。
在对尾数进行规范化处理的过程中,前导位(最左侧)1 将被删除,因为它始终为 1,只有在必要时(此处并非如此)才将其长度调整为 52 位。
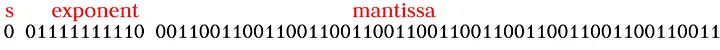
同样,用同样的方法,0.3 可以表示为
![]()
# 将两个值相加
1.平衡指数
由于我们有 0.6 和 0.3 这两个值,因此必须将它们相加。但在此之前,要确保指数相同。在这种情况下,它们不相等。因此,我们需要调整它们,将较小的指数与较大的数值相匹配。
0.6 的指数=>-1 0.3 的指数=>-2,我们必须将 0.3 与 0.6 配对,因为 0.6 的指数大于 0.3。
这里的差值为 1,因此 0.3 的尾数需要右移 1 位,指数代码增加 1 以匹配 0.6。
将尾数移动 1 位会导致最小有效位丢失,以保持 64 位标准,这可能会带来精度误差。

2.尾数加法
由于现在指数相等,我们需要对尾数进行二进制加法。
现在的值将是 0; 01111111110; 1.11001100110011001100110011001100110011001100110011001100110011001100
3.对得到的尾数进行归一化和四舍五入
在本例中,尾数已经归一化 [前导位为 1],因此跳过这一步。
最后,0.6+0.3 的结果表示为
![]()
因此,现在我们得到的结果是 0.6 + 0.3,它以 64 位 IEEE 格式表示,机器可读。我们必须将其转换回十进制,以便于人类阅读。
#将 IEEE 754 浮点表示法转换为十进制等价形式
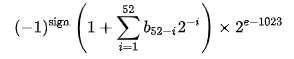
![]()
确定符号位: 0 => (-1)⁰ => +1
计算无偏指数:
(01111111110)₂ => (1022)₁₀
2^(e-1023) => 2^(1022-1023) => 2^-1
分数部分:
从尾数最左边的一位开始,将每个位的值相加,然后乘以 2 的幂。1×2^-1 + 1×2^-2 + 0×2^-3 + .......+ 0×2^-52
将这些数值代入方程并求解,得到 0.89999999999999 的结果,并显示在控制台中。[四舍五入]
=> +1 (1+ 1×2^-1 + 1×2⁻^-2 + 0×2^-3 + ....... + 0×2^-52) x 2^-1
=> +1 (1 + 0.79999999999999982236431605997495353221893310546875) x 2^-1
=> 0.899999999999999911182158029987476766109466552734375
≈ 0.8999999999999999 //numbers are rounded
//Because floating-point numbers have a limited number of digits,
//they cannot represent all real numbers accurately: when there
//are more digits, the leftover ones are omitted,i.e. the number is rounded
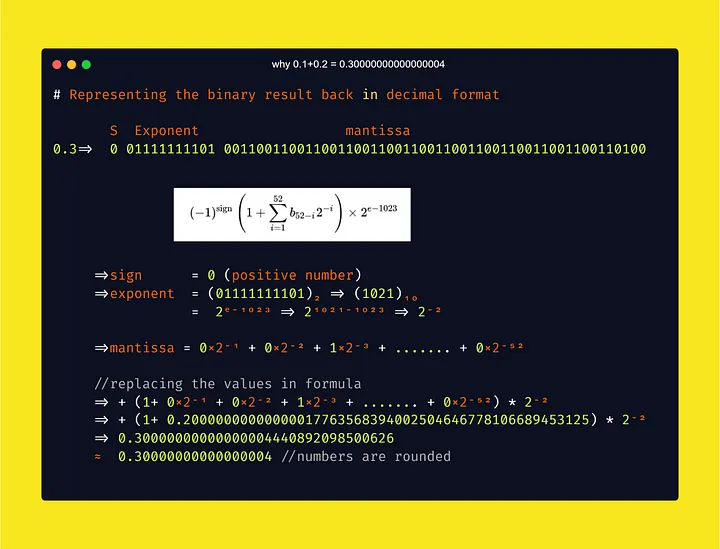
让我们再举一个例子,加深对著名表达式 0.1 + 0.2 = 0.30000000000000004 的理解。
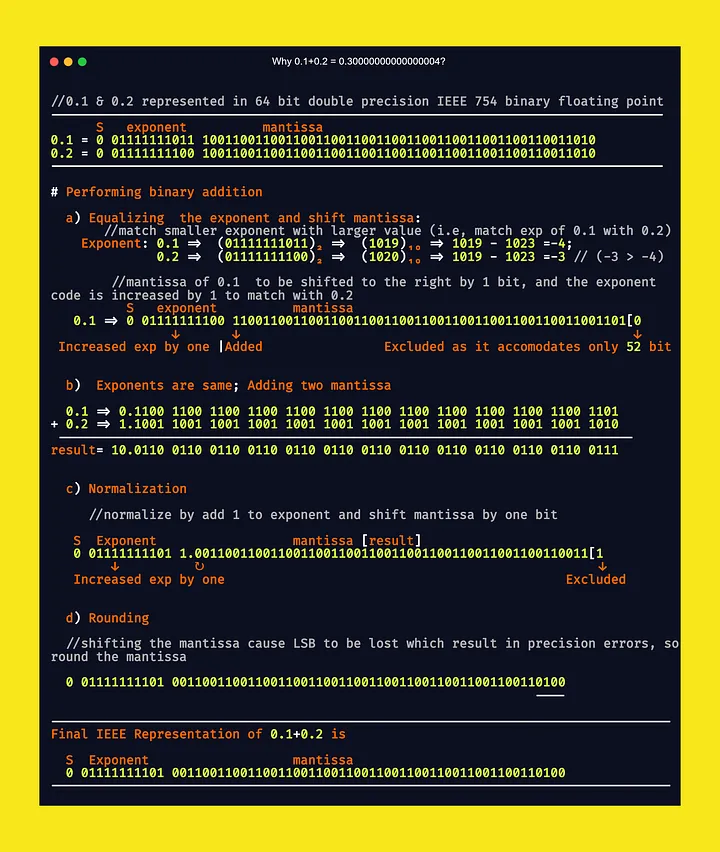
添加 64 位 IEEE 754 二进制浮点数值 0.1 和 0.2
如何解决?
让我们来看看在处理货币或金融计算的应用程序时,如何获得精确的结果,因为精确度是至关重要的。
i) 内置函数:toFixed() 和 toPrecision()
toFixed()将数字转换为字符串,并将字符串四舍五入为指定的小数位数。toPrecision()将数字格式化为特定精度或长度,并根据需要添加尾数零以达到指定精度。 parseFloat()用于删除数字的尾数零。
const num1 = 0.6;
const num2 = 0.3;
const result = num1 + num2;
const toFixed = result.toFixed(1);
const toPrecision = parseFloat(result.toPrecision(12));
console.log("Using toFixed(): " + toFixed); // Output: 0.9
console.log("Using toPrecision(): " + toPrecision); // Output: 0.9
限制
toFixed() 总是将数字四舍五入到给定的小数位,这可能不会在所有情况下都一致。 toPrecision() 也类似,但对于非常小或非常大的数字,它可能不会产生准确的结果,因为它的参数应该在 1-100 之间。
//1. Adding 0.03 and 0.255 => expected 0.283
console.log((0.03 + 0.253).toFixed(1)) // returns 0.3
//2. Values are added as a string
(0.1).toPrecision()+(0.2).toPrecision() // returns 0.10.2
ii) 第三方库
有各种库(如 math.js、decimal.js、big.js)可以解决这个问题。每个库都根据其文档发挥作用。这种方法相对更好。
//Example using big.js
const Big = require('big.js');
Big.PE = 1e6; // Set positive exponent for maximum precision in Big.js
console.log(new Big(0.1).plus(new Big(0.2)).toString()); //0.3
console.log(new Big(0.6).plus(new Big(0.3)).toString()); //0.9
console.log(new Big(0.03).plus(new Big(0.253)).toString()); //0.283
console.log(new Big(0.1).times(new Big(0.4)).toString()); //0.04
结论
用于存储十进制数的 IEEE 754 标准可能会导致微小的差异。可以使用各种库来获得更精确的结果。根据应用需求选择合适的方法。其他语言中也有类似的软件包,如 Java 的 BigDecimal 和 python 的 Decimal。
本文文字及图片出自 Decoding Why 0.6 + 0.3 = 0.8999999999999999 in JS and How to Solve?